Field of Stochastic Finance
The central objectives of Stochastic Finance are the description and analysis of the stock markets, the interest markets and the credit markets respectively. In particular this contains the evaluation of financial products which are offered and asked in the markets referred above. Moreover one is interested in quantitatively gathering and controlling risk associated with trading financial products and in analysing the patterns of yield and risk.
The consideration of the future price development of financial assets (e.g. shares) at the markets is fundamental for all aforementioned intentions. In order to map the price development adequately the temporal dynamics and the uncertainty of information should be incorporated. For these purposes specific stochastic processes corresponding to an underlying distribution are consulted in financial market models. The processes can be differentiated e.g. by continuous paths, exhibited jumps or the property of mean reversion. Subject to the number of stochastic influencing variables the models are referred to as single- or multi-factor models.
In this manner we can simulate the development of a stock index such as the S&P 500 over a timespan of several years and provide a graphical representation of the result.
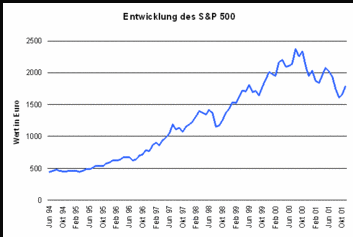
The simulation is usually based on a model which can e.g. be defined by means of a stochastic differential equation.
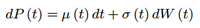
Subsequent to the phase of modelling, in which the structural approach is determined, the free parameters are fitted by means of statistical procedures (maximum likelihood, Kalman filter, LSE method, ...) on the basis of market data (phase of fitting the parameter). The implicit adjustment results from the consideration of present market prices of the modelled assets whereas the historic adjustment is based on data of the past.
The adjusted model can now be implemented and applied. For example it can be used to price derivatives whose underlying asset is priced by the model. We can illustrate the payoff profile of a derivative in a payoff diagram.
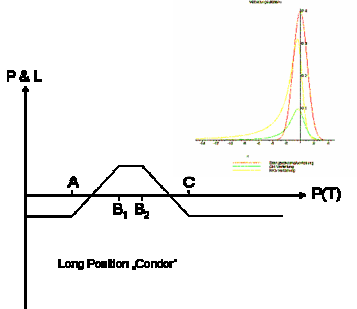
Furthermore the deduction of risk ratios being consistent with the model is conceivable. These risk measures serve as foundation for controlling and managing respective for reducing market risks. While pricing financial derivatives there often exist no closed valuation formulas. At this point the Computational Finance takes up determining approximated solutions by means of numerical methods and simulation techniques. Within the scope of risk management both private and institutional investors try to compose a portfolio of marketable assets that approaches best their individual preferences concerning risk and yield. The Financial Optimization deals essentially with this class of problems.
Current topics at the Chair of Mathematical Finance in the field of Stochastic Finance are:
- design of stochastic volatility models
- risk analysis in Lévy-markets
- portfolio optimization in incomplete markets
- hybrid credit risk models
- credit risk models with incomplete information