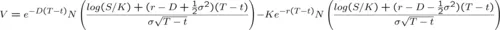Field of Computational Finance

Various kinds of models were developed in mathematical finance. Examples are prices for American options, interest rate models, default models and portfolio optimization. In practice, the pure formular and abstract mathematical formulation is rarely needed. It is a common desire to compute numbers with the model. Without the ability to solve the mathematical equations, most models would be useless for applications. A derivatives trader for example wants to know a theoretical price and perhaps how to reduce his risk before he completes a trade.

There are several challenges for an application of a mathematical model in practice. On the one hand, the input data has to be estimated. This is an econometric problem. On the other hand, the abstract model has to be implemented in a computer program. In order to implement the model, problems from the areas computer science, optimization and numerical computations occur. This is the area of Computational Finance. Furthermore, the models are extended to produce efficient and practical solutions.

People were interested in the fair value of a European Call option for a long time. Similar types of options were already traded in the 17th century. However, it took until 1973 to formulate a consistant theory of option pricing. Nowadays, many different ways are known to compute this fair value. In the following we will present the main methods.

1. Solution of the Black-Scholes-Merton formular (symbolic solution) [1]

2. Implementation of the Cox-Ross-Rubenstein binomial tree [2]

3. Risk neutral Monte-Carlo simulation [3]

4. Solution of the Black-Scholes equation (PDE) by discretization and e.g. finite differences [4]

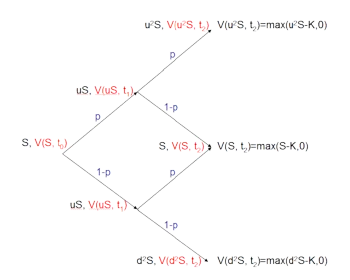
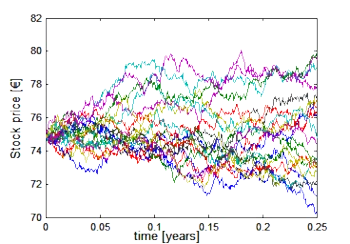
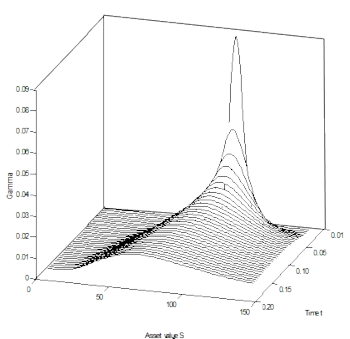
All these solution techniques have different advantages and disadvantages. The symbolic solution is easy to implement and fast to compute but not flexible in the payoff function. The binomial tree is easy to understand and flexible in the payoff. Monte Carlo Simulations and PDE methods are easy to gereralize to realistic scenarios. Which method is best depends on the concrete problem and boundary conditions such as computer memory or CPU time.

Recent topics at the Chair of Mathematical Finance in the field of computational finance are:

path-dependent options (pricing and hedging of Asian and Parisian options)
complex agreements for convertible bonds (moving windows, notice periods)
options on macro-economic indices (economic derivatives)
combinations of Monte Carlo simulation with PDE solution

Literature:

[1] Fischer Black and Myron Scholes: "The pricing of options and corporate liabilities", Journal of Political Economy, 1973, No. 81, p. 637-659

[2] John Cox, Stephen Ross and Mark Rubenstein: "Option pricing: A Simplifyed Approach", Journal of Financial Economics, 1979, No. 7, p. 229-263

[3] Phelim P. Boyle: "Options: A Monte Carlo Approach", Journal of Financial Economics, 1977, No. 4 (3), p. 323-338

[4] Paul Wilmott: "Paul Wilmott on Quantitative Finance", John Wiley & Sons Ltd., 2000, West Sussex, England