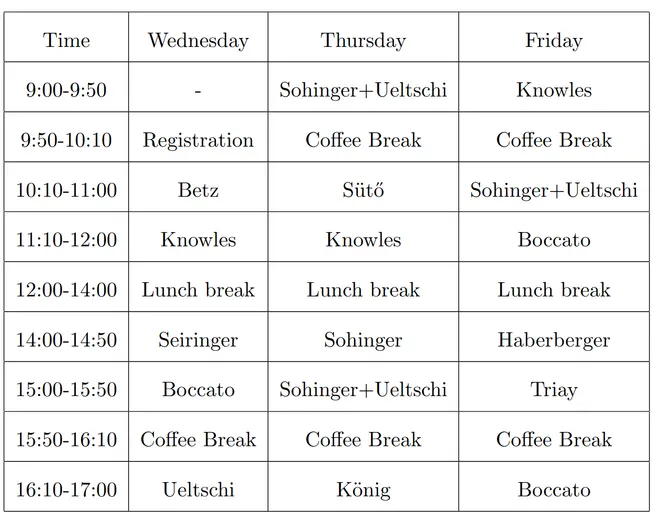
Sponsored by the SFB/TRR 352 „Mathematics of Many-Body Quantum Systems and Their Collective Phenomena“, DMV-Fachgruppe Stochastik, Global Challenges for Women in Math Science
(If the link does not work, please try a different device or browser.)
Abstracts:
Betz: Using the Feynman-Kac representation, the problem of proving offdiagonal long range order (and thus Bose-Einstein condensation) for systems of interacting bosonic particles can be re-phrased in a way that resembles (but is not equal to ) a model of classical statistical mechanics. In this overview talk, I will briefly sketch this connection, and then talk this and about various related models.I will discuss what is known about them, and outline some of the many unsolved problems connected to them.
Boccato: Bogoliubov's effective theory of 1947 provides deep insight into the low energy behavior of systems of interacting bosonic particles. Assuming that the ground state exhibits Bose-Einstein condensation, it provides expressions for the ground state energy and the excitation spectrum and predicts superfluidity. I will show how in a dilute limit (the Gross-Pitevskii scaling regime) Bogoliubov's predictions can be proven by implementing a systematic description of correlation effects.
These are joint works with C. Brennecke, S. Cenatiempo, A. Deuchert, B. Schlein and R. Seiringer.
Haberberger: We consider a low density Bose gas interacting through a repulsive potential in the thermodynamic limit. We justify, as a rigorous lower bound, a Lee–Huang–Yang type formula for the free energy at suitably low temperatures, where the modified excitation spectrum leads to a second order correction of the same order as the Lee–Huang–Yang correction to the ground state energy. Joint work with C.Hainzl, R.Seiringer, P.T.Nam, A.Triayany-body dynamics.
Knowles: Euclidean field theories have been extensively studied in the mathematical literature since the sixties, motivated by high-energy physics and statistical mechanics. In these lectures I explain how they arise as high-density limits of interacting Bose gases at positive temperature. I focus on field theories with a nonlocal quartic interaction in dimensions \leq 3, and with a local quartic interaction in dimension 2. Owing to the singularity of the free field in dimensions higher than one, the interaction is ill-defined and has to be renormalized using infinite mass and energy counterterms. The proof is based on a new functional integral representation of the interacting Bose gas. Based on joint work with Jürg Fröhlich, Benjamin Schlein, and Vedran Sohinger.
König: We consider an interacting mean-field Bose gas in general dimension in the semi-classical limit at positive temperature. That is, a trap keeps $N$ particles in a bounded part of the space, and every pair interacts on finite scale, and we put an additional factor $\frac 1N$ in front of the interaction, and the Planck constant is replaced by $N^{-1/d}$. In this regime, all the three terms (kinetic, trap and interaction energy) are on the same scale $N$.
We apply large-deviation analysis from probability theory to derive a variational formula for the limiting free energy of the system for pretty general trap and interaction potential. In the special case that was recently analysed by Deuchert and Seiringer (2021) ($d=3$, harmonic trap and not too strongly curved interaction potential), our formula concides with their formula. Our starting point is a famous trace formula in the spirit of Feynman--Kac, which enables us to describe the spatial distribution of all particles in cycles of a given length. We give evidence that the spatial distribution of the long cycles corresponds to the one of the condensate. (joint work with Marek Biskup, Los Angeles
Seiringer: We review some of the work in Mathematical Physics on dilute quantum gases and Bose-Einstein condensation during the last two decades, and discuss open problems and challenges.
Sohinger: We study interacting quantum Bose gases in thermal equilibrium on a lattice. In this framework, we establish convergence of the grand-canonical Gibbs states to their mean-field (classical field) and large-mass (classical particle) limit.
Our analysis is based on representations in terms of ensembles of interacting random loops, namely the Ginibre loop ensemble for quantum bose gases and the Symanzik loop ensemble for classical scalar field theories. For small enough interactions, we obtain corresponding results in the infinite volume limit by means of cluster expansions. This is joint work with Jürg Fröhlich, Antti Knowles, and Benjamin Schlein.
Sütő: I sketch the proof of Bose-Einstein condensation for pair potentials that are both positive and positive-type.
Triay: We study a dilute system of N interacting bosons in the Gross-Pitaevskii regime coupled with 1 impurity particle. We derive an expansion of the ground state energy up to order one and show that the excitation spectrum of the N+1 system is given by the renormalized Bogoliubov-Fröhlich Hamiltonian. This is joint work Jonas Lampart.
Ueltschi:In 1953 Feynman suggested that Bose-Einstein condensation is related to the presence of long cycles in what is now known as the Feynman-Kac representation. Suto proved equivalence in the case of non-interacting systems (1993 and 2002). He recently proposed a proof for interacting systems. I will discuss a lattice model where Bose-Einstein condensation can be excluded, and yet infinite cycles are likely. This seems to bring a contradiction. I hope for constructive feedback from the audience, that could shed light on this question.