Research Group Data Science
Our research group works towards a mathematical understanding and a mathematics driven development of data science methods connected to a variety of applications.This is done using different mathematical tools, taken from many different fields of mathematics such as Optimization, Numerical Analysis, Harmonic Analysis, Probability and Statistics, Optimal Transport theory, Theory of PDEs.
The research group is organized into three subgroups: the Applied Data Science group (Prof. Donna Ankerst), the Optimization and Data Analysis group (Prof. Felix Krahmer) and the Applied Numerical Analysis group (Prof. Massimo Fornasier). In addition the Mathematical Imaging & Data Analysis group (Dr. Frank Filbir) at Helmoltz Munich is associated to our research group.
Topics
Our Research works on a variety of different topics, ranging from theoretical foundations to algorithms and applications. An overview of some of the topics we have recently been working on can be found in the following:
Neural Networks
In order to model neural networks and interpret their training in mathematical terms, a connection between Deep Learning and Optimal Control theory can be established. Particularly structured neural networks can be described by an ordinary differential equation or even a partial differential one, and their training can be recast differently using well-known and established results such as the Pontryagin Maximum Principle. Also, their expressivity can be studied from this perspective to shed some light on some interesting behaviors of NN such as their surprising ability to generalize.
Clinical risk prediction, validation and communication
Clinical risk prediction models have become a mainstay in practice, with methodologic research now focused on maximizing their power through optimal handling of missing data on the development end and personalized interfaces on the user end. Multiple external validation has also witnessed a rise with new objectives to separate transportability from reproducibility. Research in this group focuses on the development of statistical methodology and visualization for state-of-the-art approaches to clinical risk prediction, validation and communication.
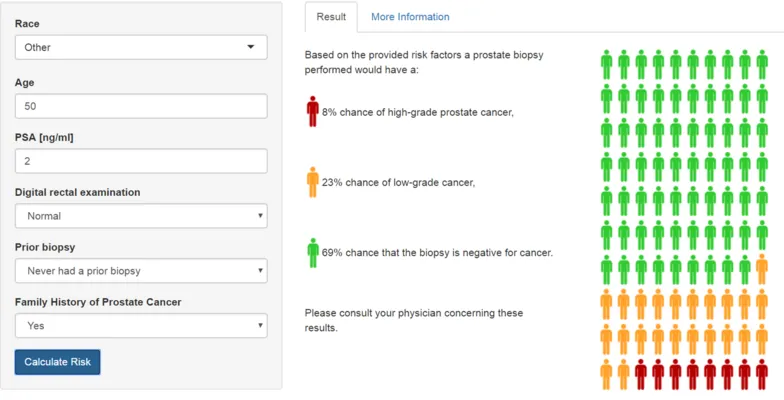
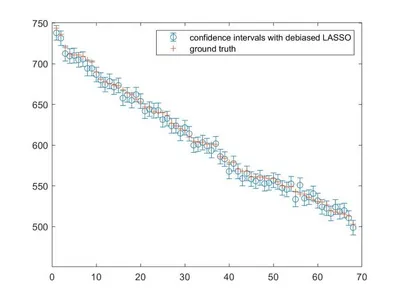
Uncertainty Quantification for High-Dimensional Inverse Problems
In many high-dimensional Inverse Problems, such as the retrieval of a Magnetic Resonance Image (MRI), the estimators are non-linear and given as solutions of optimization routines. The goal of this research path is to characterize how accurate these estimators are by using some probabilistic tools, a technique that is known as Uncertainty Quantification. This is particularly important in safety-critical applications such as autonomous driving or medical imaging. The results obtained in this group established UQ for certain high-dimensional problems which, in turn, allow for the evaluation of the accuracy of fast methods for MRI reconstruction.
Compressed Sensing
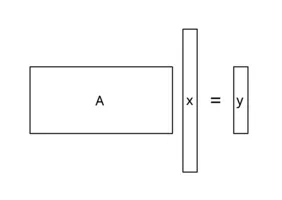
When sending a signal or measuring an object, usually, only a transformed version of the original signal is obtained. In some cases this is desired (e.g., to reduce the file size when storing photos or sending messages), in other cases it can not be avoided (e.g., when using a MRI machine).
The underlying problem is recovering the large original signal from a rather small measurement. In the standard case of a linear system, this corresponds to solving an underdetermined system Ax=y where the dimension of the unknown signal vector x is way larger than the dimension of the measurement vector y.
A challenge which can not be solved in general.
In our compressed sensing projects, we work an various applications with a wide range of different measurement operators. Our main goal is developing efficient recovery algorithms with comparably small restrictions on the signal and underlying measurement operator.
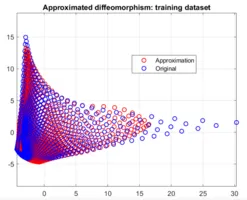
Approximation Theory for Wasserstein Sobolev Spaces
The research focus lies on a mathematical profound and robust approximation of functions, such as the Wasserstein distance, in Wasserstein Sobolev spaces. Thereby, those approximations shall be /computable/, and may indeed be obtained by deep neural networks.
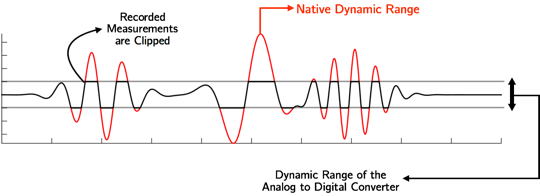
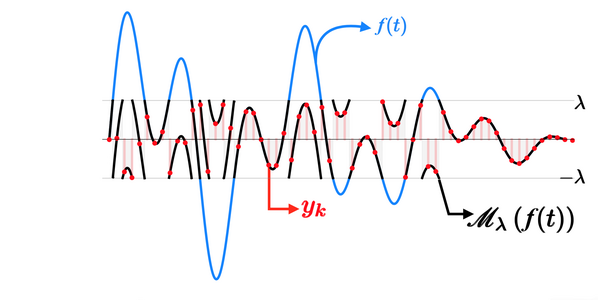
Unlimited Sampling
A major result in the field of Digital Signal Processing is the
Nyquist-Shannon Theorem, which allows for the reconstruction of a
time-continuous signal from its samples. However, circuits used for its
realization may suffer from a severe Dynamic Range (DR) bottleneck that
leads to data loss during the acquisition process.
Because of that, state-of-art approaches to the reconstruction problem are decoupled on their hardware and software sides. Our research group is working on both of them, taking care of the folding process of the samples
inside the circuit's DR, avoiding data loss; and on the unfolding process problem.
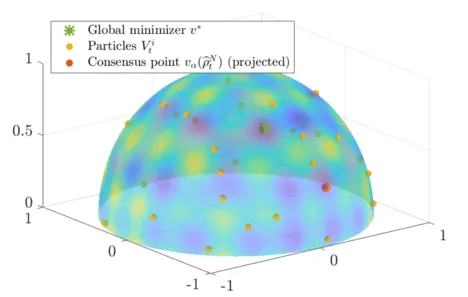
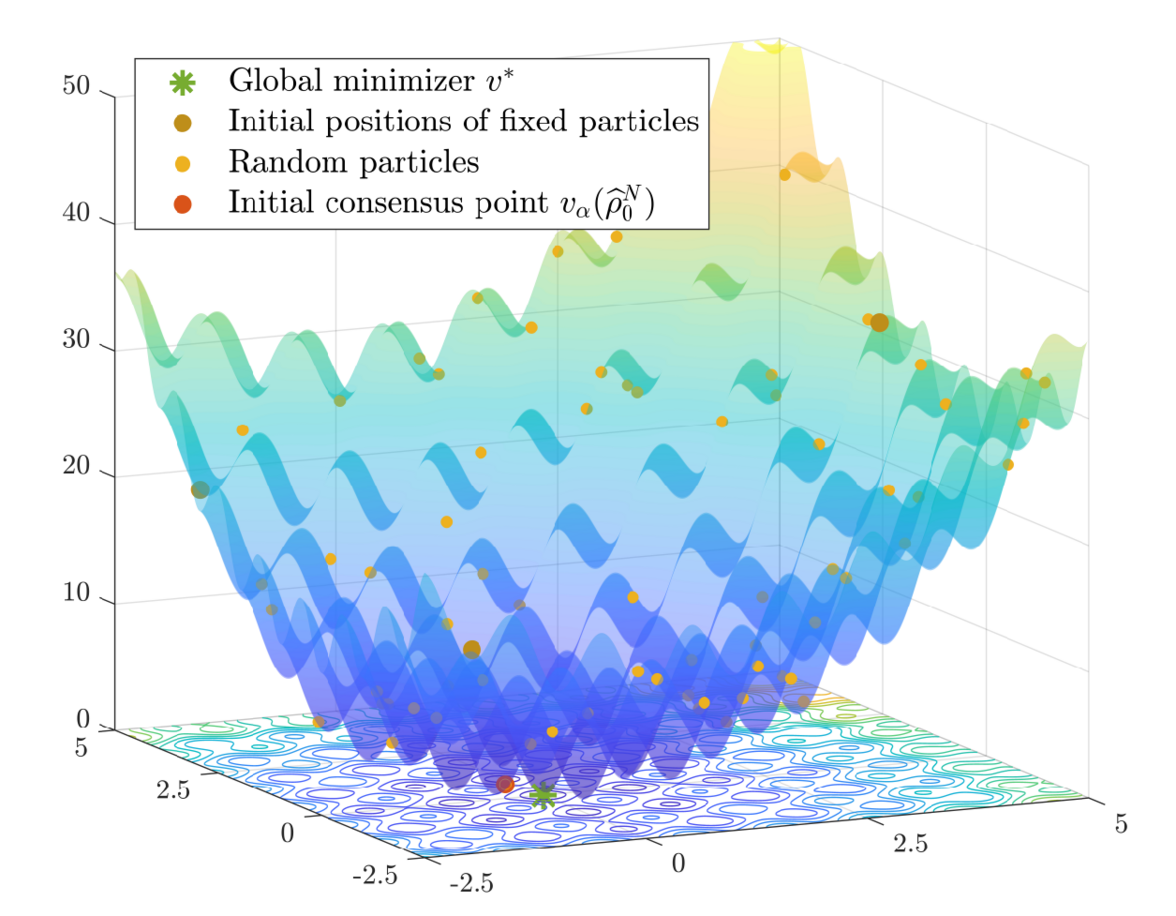
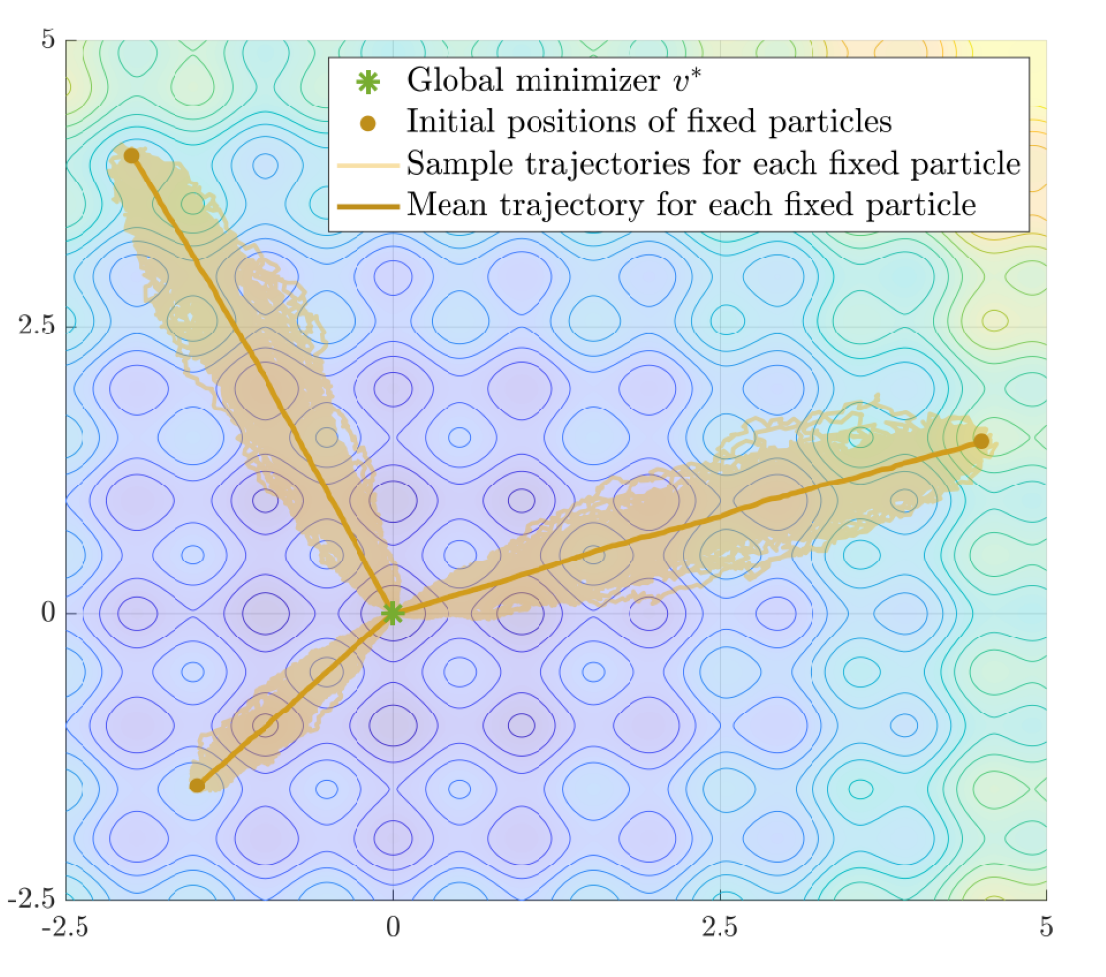
Consensus-based Optimization
The global minimization of a potentially nonconvex nonsmooth cost function living in a high-dimensional space is a long-standing problem in applied mathematics.
Consensus-based optimization (CBO) is a multi-particle derivative-free optimization method that can provably find global minimizers of such functions with probabilistic convergence guarantees.
The algorithm is in the spirit of metaheuristics with a working principle inspired by consensus dynamics and opinion formation.
More rigorously, CBO methods use an ensemble of finitely many interacting particles, which is formally described by a system of discretized stochastic differential equations, with the aim of exploring the energy landscape of the objective and by collaboration forming a global consensus about the location of the global minimizer.
At our chair we focus on different facets related to obtaining a deeper understanding of CBO as well as its relation with well-known methods such as Simulated Annealing, Particle Swarm Optimization and Stochastic Gradient Descent.
Amongst others this includes rigorous convergence analyses of the method on both the plane and on hypersurfaces, which involves technical tools from stochastic analysis and the analysis of partial differential equations.
In addition we work on efficient implementations and improvements to the dynamics in order to make the method accessible to a broader audience, in particular since CBO proved successful in various different real-world inspired application in data science, signal processing and machine learning.
Quantization of Signals and Images
One of the issues addressed by the group concerns the quantization of images and signals. Quantization refers to the process of mapping "large" and unlimited sets into a "small" and finite set. These maps are very useful from an engineering perspective for so-called analog-to-digital converters, but they are also much exploited in imaging. The group currently works by studying signals defined on manifolds with the aim of printing images on them. Halftoning techniques are also exploited to achieve this, whereby an attempt is made to represent continuous images in sequences of dots so that the image is indistinguishable when viewed from a certain distance.
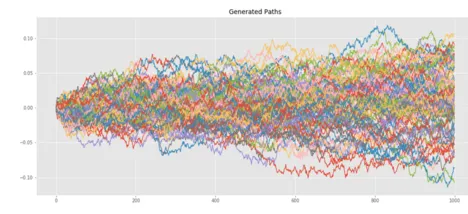
Signatures of Paths
This line of research is related to the Signature which is a mathematical tool to encode multidimensional processes or time series. It takes elements in the tensor space and consists of iterated integrals against the process. In this way, it is possible to encode essential characteristics of the underlying process which can be used as features for machine learning models for example. In this context the group investigates the behavior of the Signature w.r.t. to different sampling techniques and approximations of the paths.