Problem setting and motivation
Analysis and Numerical Simulation of Tumor Growth Models
Problem setting and motivation
We consider a solid tumor mass \(\mathcal{T}\) evolving in the interior of a domain \(\Omega\subset\mathbb{R}^d\), \(d \leq 3\), over a time period \([0,T]\). At each point \(x\in\Omega\), several cell species and other constituents exist which are differentiated according to their volume fractions, \(\phi_\alpha\), \(\alpha=1,2,\ldots,N\). The volume fractions of tumor cells is given by the scalar-valued field \(\phi_T=\phi_T(x,t)\) and the volume-averaged velocity is denoted by \(v\). The mass density of all \(N\) species is assumed to be a single constant field, and the evolution of the tumor cells is governed by the evolution of proliferative cells with volume fraction \(\phi_P\), hypoxic cells \(\phi_H,\) and necrotic cells \(\phi_N\). The nutrient supply to the tumor is characterized by a constituent with volume fraction \(\phi_\sigma=\phi_\sigma(x,t)\).
A most basic four species tumor growth model involving the tumor cells, the healthy cells ,the nutrient-rich extracellular water and the nutrient-poor extracellular water can be sketched as follows:
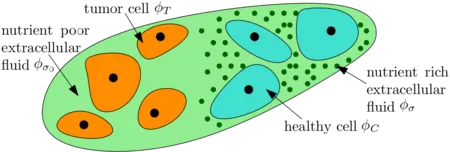
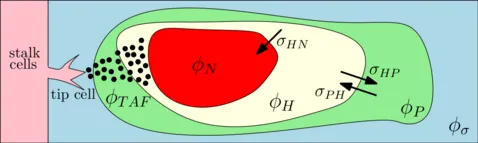
Separating ϕT further into proliferative, hypoxic, necrotic cells and involving angiogenesis gives the following sketch:
Prominent among more recent proposed models are those involving diffuse-interface or phase-field representations designed to capture morphological instabilities in the form of phase changes driven by cell necrosis and non-uniform cell proliferation. These effects result in tumor growth made possible by increases in the surface areas at the interface of cell species. Models that can replicate such phenomena usually involve Ginzburg-Landau free energy functionals of species concentrations or volume fractions, nutrient concentrations, and, importantly, gradients of species concentrations as a representation of surface energies, a feature that leads to Cahn-Hilliard type models. The use of such phase-field formulations eliminates the need for enforcing conditions across interfaces between species and for tracking the interface, the locations of which are intrinsic features of the solution. Such non-sharp interfaces are often better characterizations of the actual moving interfaces between multiple species within a tumor than models employing sharp interfaces.
We introduce a general class of multispecies, phase-field models developed from balance laws and accepted cell-biological phenomena observed in cancer, in which cell velocity, present in mass convection, is modeled via at time-dependent, nonlinear flow field governed by a Darcy-Forchheimer-Brinkman law, which can be obtained by the means of mixture theory. This model involves nonlinear characterizations of cell velocity obeying a time-dependent Darcy-Forchheimer-Brinkman law.
$$\partial_t \phi_T+ \text{div}(\phi_T v) = \text{div} (m_T(\phi_T,\phi_\sigma) \nabla \mu) +\lambda_T\phi_\sigma \phi_T(1-\phi_T)-\lambda_A\phi_T,$$
$$\mu = \Psi'(\phi_T)-\varepsilon_T^2 \Delta \phi_T -\chi_0 \phi_\sigma$$
$$ \partial_t \phi_\sigma + \text{div}(\phi_\sigma v)= \text{div}\big(m_\sigma(\phi_T,\phi_\sigma) (\delta_\sigma^{-1} \nabla \phi_\sigma - \chi_0 \nabla \phi_T)\big) -\lambda_\sigma\phi_T\phi_\sigma,$$
$$\partial_t v + \alpha v = \text{div} (\nu(\phi_T,\phi_\sigma) \text{D} v)- F_1 |v| v - F_2 |v|^2 v - \nabla p + (\mu+\chi_0\phi_\sigma) \nabla \phi_T,$$
$$ \text{div}\ v = 0.$$
Analytical Results
Theorem (Existence of global weak solutions).
Let the following assumptions hold:
(A1) \( \Omega \subset \mathbb{R}^3 \) is a bounded Lipschitz domain and \( T>0.\)
(A2) \( \phi_{T,0} \in H^1, \phi_{\sigma,0} \in L^2, v_0 \in H.\)
(A3) \( m_T,m_\sigma,\nu \in C_b(\mathbb{R}^2) \) such that \( m_0 \leq m_T(x),m_\sigma(x),\nu(x) \leq m_\infty \) for positive constants \( m_0,m_\infty<\infty.\)
(A4) \( \Psi \in C^2(\mathbb{R}) \) is such that \( \Psi(x)\geq C (|x|^2-1), |\Psi'(x)| \leq C(|x|+1), \)and \( |\Psi''(x)|\leq C(|x|^4+1).\)
Then there exists a weak solution quadruple \((\phi_T, \mu, \phi_\sigma, v)\) of the tumor growth model above. Moreover, the solution quadruple has the regularity:
$$ \phi_T \in H^1(0,T;(H^1)') \cap C([0,T];L^2) \cap C_w([0,T];H^1),$$
$$ \mu \in L^2(0,T;H^1),$$
$$ \phi_\sigma \in W^{1,4/d}(0,T;H^{-1}) \cap C([0,T];H^{-1}) \cap C_w([0,T];L^2) \cap (1+L^2(0,T;H_0^1)),$$
$$ v \in W^{1,4/d}(0,T;V') \cap C([0,T];V') \cap C_w([0,T];H) \cap L^4(0,T;[L^4]^3) \cap L^2(0,T;V). $$
Additionally, there is a unique p∈W−1,∞(0,T;L20) such that (ϕT,μ,ϕσ,v,p) is a solution quintuple in the distributional sense.
Numerical Results

Publications
A selection of publications from our chair dealing with topics from tumor growth models.