Methods for Large Scale Simulations
The surface of our planet is shaped by processes deep beneath our feet. Phenomena like earthquakes, plate tectonics, crustal evolution up to the geodynamo are governed by forces in the Earth's mantle. These are part of a planetwide solid-state convection that transports heat from the interior of our planet to its surface. For this reason, the study of the dynamics of the mantle is critical to our understanding of how the entire planet works.
There is a constant demand for ever more realistic mantle convection models (MCMs). This includes, e.g., compressible flow formulations, strongly non-linear rheologies, i.e., models in which the fluid viscosity depends not only on pressure and temperature, but also on the strain-rate, the inclusion of phase transitions or the tracking of chemical composition.
Such models are subject to sudden changes of material properties. For instance, steep temperature gradients between cold, subducting slabs and hot mantle material yield abrupt changes in the temperature-dependent viscosity of several orders of magnitudes. This dictates spatial resolutions for the MCM that tend towards ∼1 km.
Another trend is the growing use of MCMs to perform inverse computations via adjoint techniques in order to link uncertain geodynamic modeling parameters to geologic observables and, thus, improve our understanding of mantle processes.
These advanced models require efficient software frameworks that allow for high spatial resolutions and combine sophisticated numerical algorithms with excellent parallel efficiency on supercomputers to provide fast time-to-solution.

Interdisciplinary work
The presented work requires a careful co-design and expertise of many disciplines and can not be stemmed by mathematicians alone. Therefore, we interdisciplinarily work with partners from computer science and geophysics
- Prof. Dr. Ulrich Rüde: Head of the Chair of Computer Science 10 (System Simulation) at the Friedrich–Alexander University Erlangen–Nürnberg
- Prof. Dr. Hans-Peter Bunge: Professorship for Geophysics at the Ludwig Maximilian University of Munich
Problem setting and motivation
A general mathematical description of mantle convection can be derived from
the principles of conservation of momentum, mass and energy. A simplified mantle convection model with non-dimensionalized velocity \(\mathbf{u}\), pressure \(p\) and temperature \(T\)
is given
$$
-\mathop{\mathrm{div}} (\nu (\nabla \mathbf{u} + (\nabla \mathbf{u})^\top) + \nabla p = -\mathtt{Ra}\,T\,\mathbf{e}_r \quad \text{in } \Omega \times I
$$
$$
\qquad\qquad\qquad\qquad -\mathop{\mathrm{div}} (\mathbf{u}) = 0\phantom{\mathbf{R}\,} \quad \text{in } \Omega \times I
$$
$$
\quad\qquad\qquad\partial_t T + \mathbf{u} \cdot \nabla T - \Delta T = 0\phantom{\mathbf{R}\,} \quad \text{in } \Omega \times I
$$
in the space-time domain \(\Omega\times I\), where \(\nu = \nu(\mathbf{x}, T)\) is the temperature and spatial variable (\(\mathbf{x} \in\Omega\)) dependent
viscosity, \(\mathbf{e}_r\) is the gravitational unit vector pointing to the center of the sphere, \(\mathtt{Ra}\) the Rayleigh number, which characterizes the influence of the convection in the mantle.
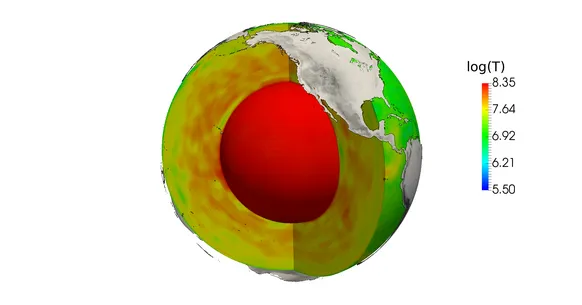
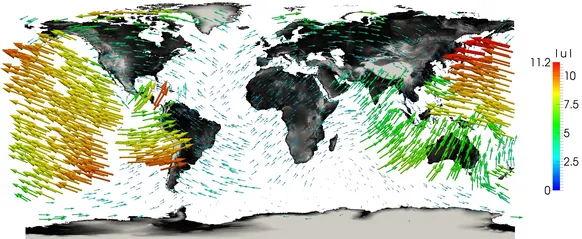
By a mineralogical model, where a tomographic model of seismic wave speeds is used to measure the density within the Earth, one can obtain today's temperature (left). Moreover, by plate tectonics models make it possible to determine velocity speeds on the surface. (right)
Earth's topography is by no means constant. It is continuously changed by various processes such as erosion, sedimentation, and global isostatic adjustment. The latter being the fact that on "short" time scales Earth behaves elastically when a load, e.g.~a glacier, is added on or removed from its surface. Another important contribution is deflection of the Earth's surface as a response to viscous stresses in the mantle. This type of surface deflection is referred to as \emph{dynamic topography} and occurs both at the surface and the core-mantle boundary (CMB). Dynamic topography can serve as a proxy for mantle flow processes, and consequently can help Geodynamicists to constrain flow parameters in the mantle.
One of the parameters often neglected in geodynamic models is the presence of lateral viscosity variations (LVVs), induced mainly by thermal variations in the mantle. Originally LVVs were neglected because of the complexities arising from mode coupling in the PMT. Our \lsqpe-based FE approach, as also classical FEM, allows viscosity variations, so that we can compute models of dynamic topography including orders of magnitude in LVVs.
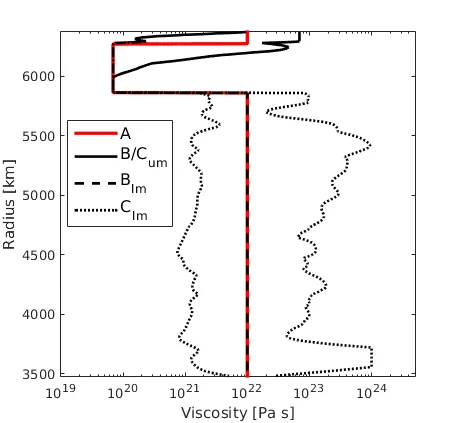
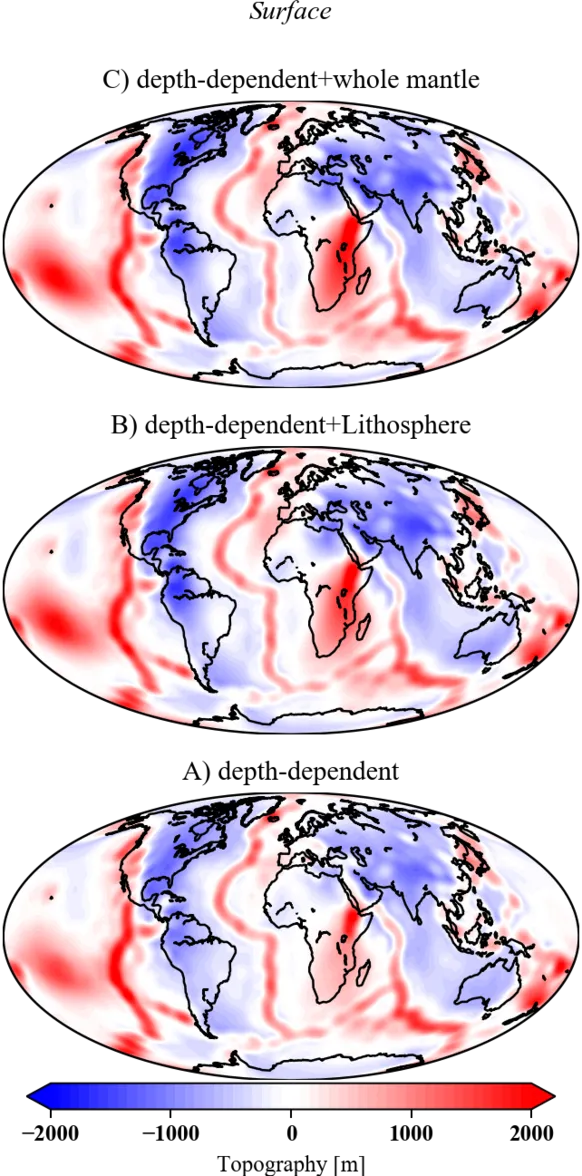
The results show a considerable effect of LVVs on the modeled dynamic topography at the Earth's surface, and CMB. The amplitudes in models with LVVs are generally increased by 20%, with changes reaching up to 50% over plate boundaries. Equally important, models with LVVs generate substantial signal in regions where the model without LVVs show no significant surface deflection.