- Analysis of Boundary Effects on PDE-Based Sampling of Whittle--Matérn Random Fields. SIAM/ASA Journal on Uncertainty Quantification 7 (3), 2019, 948--974 more…
Random Heterogeneous Media
Real materials, employed in engineering applications or that occur in nature, possess random heterogeneous microstructures, which play a crucial role in their macroscopic behavior and in determining their effective properties. The particular features of the microstructure of a material, as for example porosities, cracks, precipitates, polycrystalline shape and texture, etc., have an important impact on the lifetime of an industrial structure and highly depend on the choice of manufacturing process.
Problem Setting and Motivation
Surrogate microstructute models
A common approach to modeling random multiphase heterogeneous materials is to develop so-called surrogate models that ideally mimic key macroscale features of the material. These models approximate the geometric distribution of phases, and effective properties are calculated using homogenization techniques. Efficient sampling process makes possible the use of Monte-Carlo methods to evaluate statistical properties for the quantities of interest in a given material class. Such surrogates for two-phase materials are often used to study and to characterize properties of the porous media, e.g., permeability or effective constitutive models, in fatigue and damage analysis, in microstructure design.
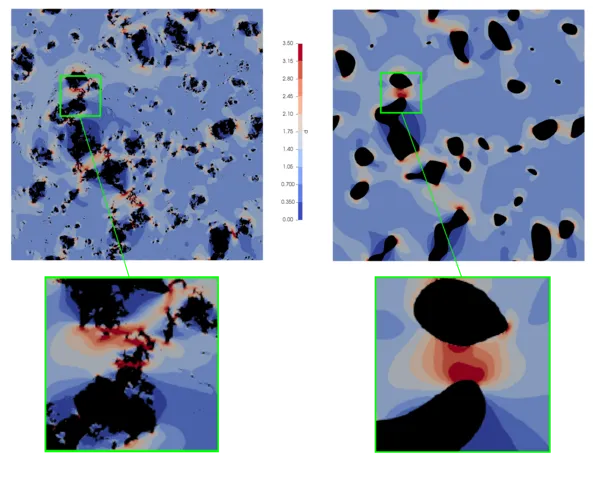
Goal-Oriented Adaptive Modeling of Random Heterogeneous Media
Methods for generating sequences of surrogates approximating fine scale models of two-phase random heterogeneous media are presented that are designed to adaptively control the modeling error in key quantities of interest. For specificity, the base models considered involve stochastic partial differential equations characterizing, for example, steady-state heat conduction in random heterogeneous materials and stochastic elastostatics problems in linear elasticity. The adaptive process involves generating a sequence of surrogate models defined on a partition of the solution domain into regular subdomains and then, based on estimates of the error in the quantities of interest, assigning homogenized effective material properties to some subdomains and full random fine scale properties to others, to control the error so as to meet a preset tolerance. New model-based Multilevel Monte-Carlo methods (mbMLMC) are presented that exploit the adaptive sequencing and are designed to reduce variances and thereby accelerate convergence of Monte-Carlo sampling. Estimates of cost and mean squared error of the method are presented. The results of several numerical experiments are discussed that confirm that substantial saving in computer costs can be realized through the use of controlled surrogate models and the associated mbMLMC algorithms.