Research

Research interests in Johannes Zimmer’s group include partial differential equations and their underlying particle models. One focus is on scale-bridging from stochastic many-particle systems to partial differential equations which describe the collective behaviour of such systems. A particular interest of our group is the thermodynamic formulation of the resulting equations in terms of evolution of energy and entropy, including variational formulations related to large deviation theory.  We are particularly fascinated by equations of fluctuating hydrodynamics, which describe fluctuations (small deviations) around the limit equation. We study these equations analytically, and utilise their structure in machine learning to infer evolution equations in form of partial differential equations from particle data. In terms of applications, we study models from mathematical physics and mechanics, for example active matter.

Specifically, these are some topics we are currently interested in.

• Derivation of thermodynamic systems from particle models: One research area of our group is the analysis of problems out of equilibrium and nonequilibrium problems and their derivation from particle models. In particular, systems can often be described by a combined evolution of energy and entropy (this is sometimes called metriplectic evolution or GENERIC, General Equation of Nonequilibrium Reversible-Irreversible Coupling). How can we derive these fields and their evolution equations from underlying particle systems describing the same system on a finer scale? Mathematical tools we employ here range from hydrodynamic limits and large deviation theory to the theory of dilations and compressions.
• Fluctuating hydrodynamics: The equations of fluctuating hydrodynamics (sometimes called Dean-Kawasaki type equations) describe stochastic perturbations around the limit equation, such as the collective motion of finitely many particles around the hydrodynamic limit describing the evolution of infinitely many particles. The stochastic partial differential equations describing fluctuating hydrodynamics are fascinating - for a wide class of systems, solutions exist precisely if the initial data is atomic, and provably no solutions exist for smooth initial data. We study such equations and suitable regularisations analytically and are interested in their numerical approximations.
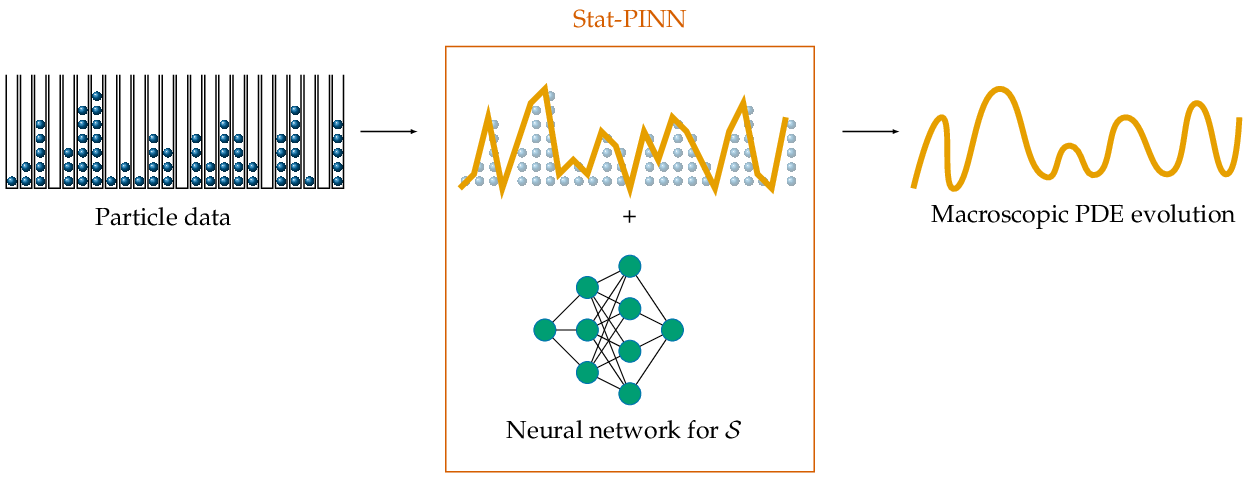
• Thermodynamics-inspired machine learning: We have derived infinite-dimensional versions of fluctuation-dissipation statements (which are relation to equations of fluctuating hydrodynamics) which allow us to learn macroscopic evolution from particle data. With Nicolas Dirr, Celia Reina and students we have developed Stat-PINNS, a machine physics-informed neural network method incorporating information from statistical mechanics to learn macroscopic evolution of a hydrodynamic limit in form of a (deterministic) partial differential equation. Both the entropy 𝒮 and its evolution operator 𝕂 are learned. Currently we are developing rigorous error estimates for this approach.
   

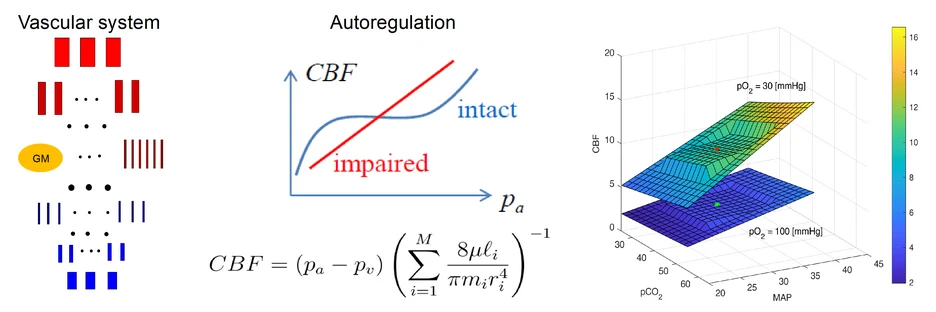
Mathematical simulations towards preventing cerebral hemorrhage in premature infants: One of the most frequent complications during the postnatal development of premature infants is intraventricular hemorrhage, which may lead to permanent disabilities. Infants born before 30 weeks of gestation or those with a birth weight below 1500 g are at risk of hemorrhage with an overall incidence of 20% to 25%. Intraventricular hemorrhage originates mostly in the subependymal germinal matrix (GM), a specific area of the developing brain that consists of highly vascularized neuroepithelial cells and a fragile capillary network. The pathogenesis of intraventricular hemorrhage is multifactorial. One of the most important factors is strong fluctuations of cerebral blood flow (CBF) caused by impaired cerebral autoregulation, which plays an important role in maintaining the required level of cerebral perfusion. The aim of the current project is the development of numerical methods for the simulation of the blood vessel system and CBF in immature brain. The cerebrovascular system of the adult brain has been the object of mathematical studies over the past 20 years. However, despite significant progress in understanding the cerebral regulatory mechanism, there is a lack of knowledge about impaired cerebral circulation in premature newborns. Therefore, creating an appropriate mathematical description of the cerebral circulation that simulates the peculiarities of the immature brain is a challenging task. We develop a mathematical model which takes into account the morphological characteristics of the blood vessels according to gestational and postnatal age. In addition, the cerebral autoregulation and dependence of CBF on variations in blood pressure, pCO₂, pO₂ and hematocrit is modeled by corresponding vascular reactivity (i.e., vasoconstrition and vasodilation). The calculated CBF will then be added to the multivariate statistical analysis as an additional independent variable to enhance the prognostic accuracy of early detection of premature infants at increased risk of hemorrhage.

This project is funded by the Klaus Tschira Foundation (Heidelberg, Germany).

The project is a joint collaboration of  Renée Lampe (Head of the Research Unit of the Buhl-Strohmaier Foundation for Cerebral Palsy and Paediatric Neuroorthopaedics at Technical University of Munich, School of Medicine, Klinikum rechts der Isar in Munich, Germany and holder of the Markus Würth endowed professorship) and Johannes Zimmer (Chair for Analysis and Modelling, School of Computation, Information and Technology)

Team members: Andrey Kovtanyuk (School of Computation, Information and Technology) and Irina Sidorenko (Klinikum rechts der Isar)