Da wir uns an ein internationales Publikum richten, ist diese Webseite nur auf Englisch verfügbar.
Research group Numerical Analysis

People | Research | Publications | Oberseminar: NumCSE
At the Chair for Numerical Analysis at TUM we bring together an abstract mathematical theory and efficient computational methods to solve problems within real world applications from science and engineering.
Our main research activities can be summarized within the three categories Modelling and Analysis, Numerical methodologies and Simulation and HPC. For more details and references about certain topics, please visit our individual research-pages.
Our Research Profile
Within the process of scientific knowledge gain, a huge interplay takes place between our three research cathegories. Starting with a real world application and a rough conceptual idea of mechanisms, as a first step a mathematical model, quantifying observations and relations is created and analyzed. Once such a model is created, solutions to the respective model equations are sought. With models becoming more and more complex for real world applications, one can usually not hope for closed, analytical solutions, but would rather employ numerical methods in order to obtain suitable approximations. Finally the efficient realization of such numerical methods on modern supercomputer hardware in order to create meaningful simulations is a field of research at the border of numerical mathematics and computer science in itself. Eventually numerical simulation results are then used to better understand the original conceptual ideas as well as their underlying scientific phenomena, which closes one iteration within the loop in the graphic aside with many more iterations of mutual improvement and optimization of the individual steps to come.
Modelling and Analysis
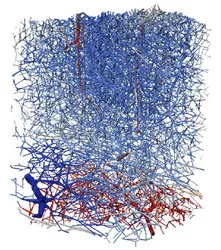
At the beginning of a scientific description of real-life and scientific observations stands a mathematical model. While such models can come in many different forms and shapes, many of them can be formulated via a set of (partial) differential equations, describing for example the flow of wind or water, the deformation of solid materials under stress or the propagation of electromagnetic waves. We at the chair for numerical analysis pursuit the mathematical analysis of such models, the derivation and development of new ones as well as their coupling and combination in order to describe complex phenomena from science and engineering.
Numerical methodologies
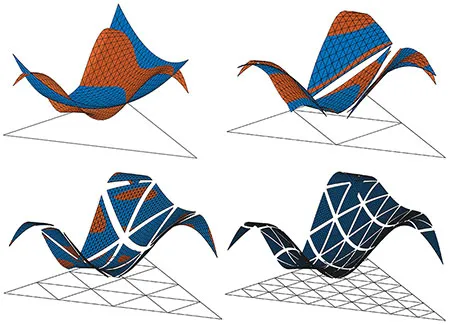
The more complex and detailed a mathematical model is, the harder the solution of its model-equations becomes, eventually requiring numerical approximation-algorithms and schemes. One of the main research areas of our group lies within the advancement of discretization techniques for partial differential equations such as the finite element method, the development of new methods for example for fractional differential equations or the generation of random materials as well as the derivation and implementation of boundary and interface conditions in order to couple different methodologies together.
Simulation and HPC

Finally, having a suitable mathematical model as well as numerical solution technique at hand, it remain the challenges of large datasets, the requirement for fine resolutions and the computational complexity associated with that. To tackle these problems we aim to utilize current supercomputing hardware by developing high performance, parallel code as well as employing efficient surrogate models. With these we eventually arrive at realistic simulations of actual real-life and scientific scenarios from the propagation of earth-mantle magma-plumes over the bloodflow-dynamics in cranial aneurysms up to the impact of earthquakes on building structures.
Within many fields of application we work in close cooperation with scientists and individual experts from these fields in order to contribute also beyond the borders between mathematics and computation, science and engineering.