Aufgrund der internationalen Ausrichtung unserer Forschungsgruppe "Statistics" ist diese Webseite nur auf Englisch verfügbar.
Statistics Research Group
A major goal in our complex world is to identify and quantify relationships such as the effects of global warming, of genes on patients health and financial turmoil on the economy. In our research group, we use statistical modeling approaches to these goals.
Principal investigators in this research group are Prof. Mathias Drton, the chair of Mathematical Statistics, and Prof. Claudia Czado, the Professorship in Applied Mathematical Statistics. The group organizes the seminar series Statistics and Data Science. For upcoming talks, please have a look at the website of the seminar.
Mathematical Statistics
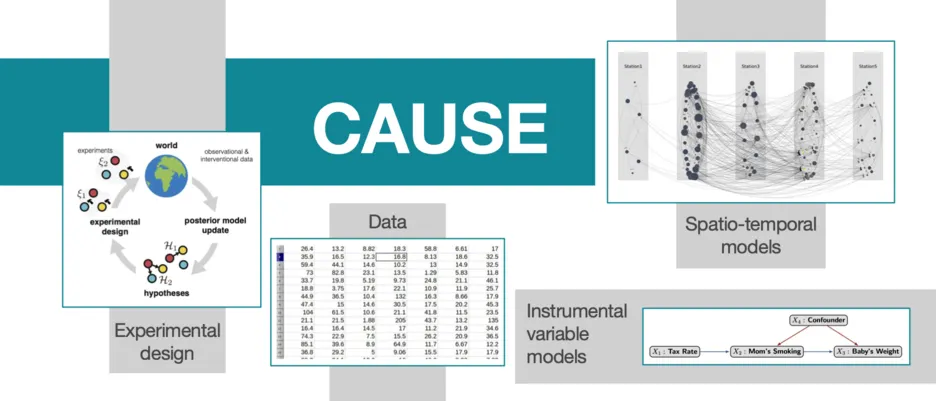
The research of our group is driven primarily by problems arising in statistical analysis of multivariate data. Much of our work is concerned with probabilistic graphical models, which use mathematical graphs and networks to represent different types of stochastic dependence among a collection of variables. In this framework, we develop new methods to assess independence relations, to infer interaction structures, and to model and estimate causal relationships. Our work is connected to a number of different areas of statistics, ranging from causal inference, high-dimensional statistics and latent variable models to the area of algebraic statistics, which is concerned with applications of algebraic techniques to study statistical models and methods.
Funding for our research has come from the European Research Council, the Mathematical Research Data Initiative (MaRDI), the Munich Data Science Institute, the TUM/ICL Joint Academic of Doctoral Studies, and the Munich Center for Machine Learning.
Applied Mathematical Statistics
We use copula based approaches to separate the marginal behavior of variables from the joint behavior. The special focus is on the theory and practical use of vine copulas. They are a flexible class of dependence models and break multidimensional dependencies into multiple bivariate building blocks. Thus, they can handle complex and high-dimensional data.
Current research areas include vine based versions of state space models, quantile regression, clustering/classification approaches and extreme risk probability estimation. More information on these theoretical developments and their applications can be found at vine-copula.org.
For the user we developed the open source software VineCopula and rvinecopulib. The book Analyzing Dependent Data with Vine Copulas“ gives a step by step introduction . A recent review on vine copula based modeling appeard in the Annual Review of Statistics and Its Application. The research is partly funded by the German Research Foundation and the Munich Data Science Institute.