Energy-corrected finite element method
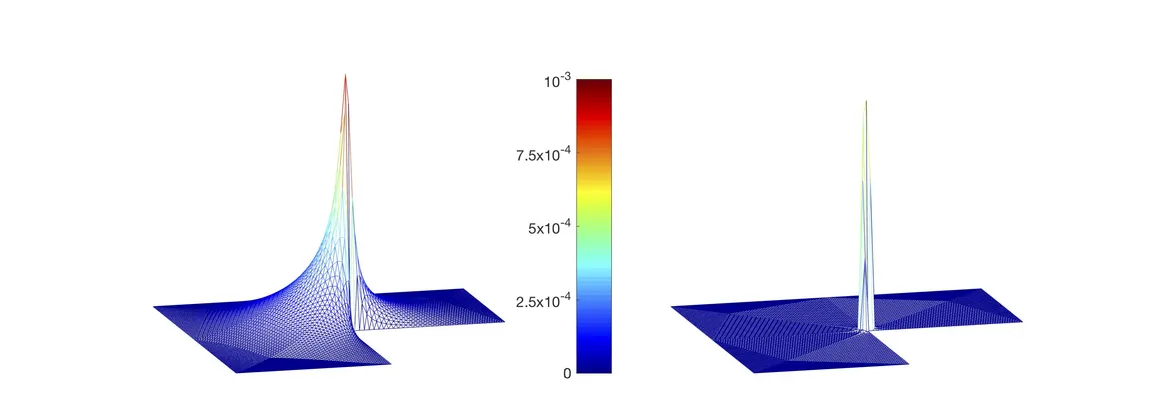
Among domains of particular interest in applied sciences are polygons, potentially including non-convex corners. The presence of corners in the computational domains negatively influences the regularity of the solutions of elliptic partial differential equations, by introducing a particular known type of singular functions into the solution. The appearance of singular functions in the solutions on polygonal domains diminishes the accuracy of the standard finite element method. Furthermore, the approximation is suboptimal not only in the vicinity of the corner but also when considered in some positive distance from it - the behaviour known as the pollution effect.
Many approaches for improving the global convergence of the finite element solution exist already, such as adaptivity, graded mesh algorithms or enrichment of the finite element space by singular functions. These methods improve the approximation quality regaining the optimal convergence properties. However, they require a modification of the standard finite element solution in a neighbourhood of the corners and require changing the structure of the mesh or the function space, in which the solution is approximated.
We propose an alternative approach - the so-called energy-correction, which is based on the observation that the approximation quality of the finite element solution when measured in the L2(Ω)-norm, is limited by the approximation of the energy. The numerical algorithm modifies the bilinear form governing the system of equations so that the optimal approximation of the energy is regained. Using the energy-correction method, optimal convergence concerning the interpolation error is regained. As opposed to the schemes involving adaptivity or the mesh grading, the energy-correction works on uniformly refined meshes. Since the method was first introduced for the scalar elliptic equations, it has been extended to the higher-order elements, parabolic problem, fluid dynamics and optimal control problems.
Stokes problem
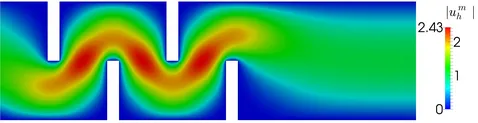
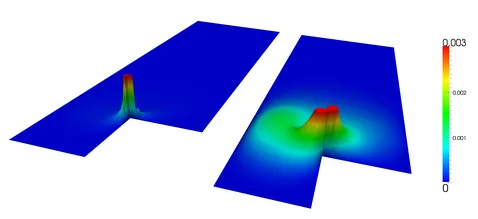
Flow problems on domains with re-entrant corners appear in many applications of interest. A typical example is the Stokes flow over a backwards-facing step. In the presence of re-entrant corners in the simulation domain, the Stokes solution will, in general, have singular components even when the data are smooth. Therefore, standard finite element approximations show poor convergence results compared to the nodal interpolation. More precisely, the pollution effect can be observed in the L2(Ω)-norm.
Parabolic problems
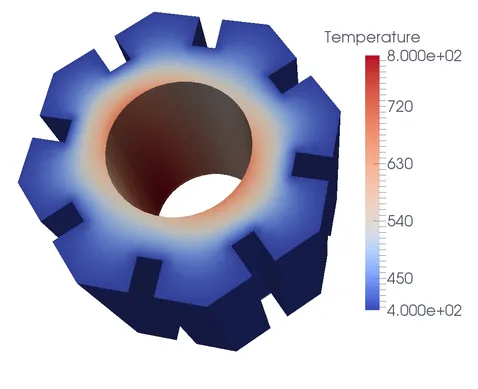
The pollution effect introduced for the elliptic partial differential equations can also be observed in the case of parabolic problems on polygonal domains. As opposed to the methods involving mesh refinement around the singular corner, the energy-correction requires only uniform triangulation of the computational domain. This results in a non-restrictive stability requirement for the explicit time-stepping schemes. We propose a discretisation of parabolic equations based on the piecewise-linear energy-corrected finite element combined with the explicit time discretisation. This scheme is completed with the mass lumping strategy yielding fast solvers in time, and an additional post-processing step. The superiority of the energy-corrected scheme can be seen not only in its qualitatively higher accuracy but also in significantly lower computational requirements. As a potential application, we applied the piecewise linear energy-corrected finite element method to a real 3D geometry of a graphite moderator brick of a nuclear power plant. Such a moderation type is commonly used in Advanced Gas-cooled Reactors (AGR). Efficient simulations of heat distribution in moderator bricks play an essential role in the analysis of the material properties of the whole nuclear core, and accurate computations of temperature distribution can help determine the lifetime of nuclear materials, which often suffer from large temperature gradients and fast neutron fluxes.